I recently purchased a brand new older than me Yaesu FT-736 ham radio transceiver on eBay from a Japanese seller. It is a nice VHF/UHF rig, with true full duplex and “all mode”s (FM, SSB, CW, packet) capabilities and a nice “facade full of dials and buttons” ergonomics that I missed a bit coming from a computer-controlled SDR.
I plan to use it to setup a satellite base station at home. The trick is that nowadays most if not all FM satellites require CTCSS tones. This transceiver can do that with a little plug-in board that was sold by Yaesu as an option back in the day. Mine does not have it unfortunately.
Original parts are nowhere to be found (or sell for a significant fraction of the price I purchased the radio…) and Piexx sells a somewhat expensive 79$ replacement board that is a modern redesign. Considering the triviality of the function of this board, I looked for homebrew schematics. Homo ludens has already done so using a PIC micro-controller but not having a PIC programmer at home, and finding the design a bit flawed I decided to design my own.
Encoding CTCSS tones
I wanted to keep the design simple and use components I was already familiar with. I pick the ATmega328P micro-controller as it was cheap, powerful enough and I already had the programmer for it. Sub-tone decoding is done using the onboard ADC and encoding is done through PWM. The schematics of the board is the following:
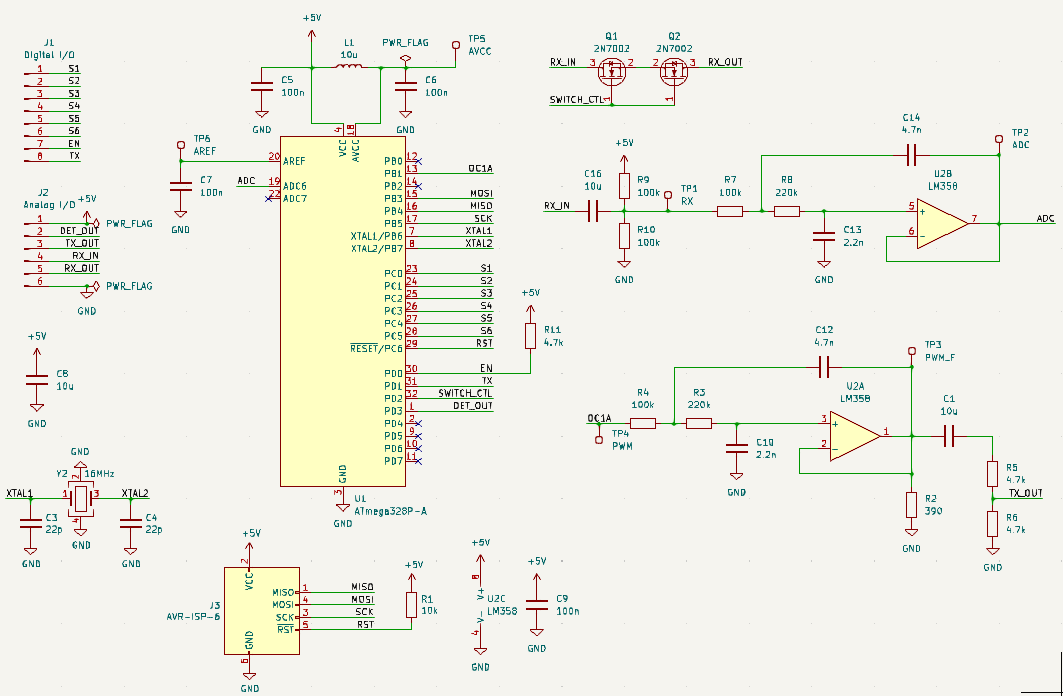
Contrary to homo ludens’ design, the PWM does not output a square wave at the CTCSS frequency. It would have made the filtering of the tone harmonics tedious for two reasons. At first, square waves have strong third harmonics, requiring sharp low-pass filters of high orders to eliminate them. Furthermore, the highest CTCSS frequency, 254.1Hz is more than thrice the lowest CTCSS frequency: the proper elimination of the third harmonics would require filter banking, in a similar way as amplifiers work when working over several bands.
In my implementation, the output frequency is 201 times the CTCSS frequency, with a PWM modulation that samples a sine wave period over 201 points. The low-pass filter must simply be designed to let the highest CTCSS tone (254.1Hz) pass, while blocking the PWM frequency of the lowest tone (13.4kHz) which is much simpler to achieve. A simple second order active filter using a Sallen-Key topology does the trick.
Decoding CTCSS tones
I don’t really need decoding capabilities in my usage of my radio. However, for the sake of the challenge of performing a feature complete re-implementation of the FTS-8 board, I wanted my board to have that.
Decoding CTCSS consist on detecting the strength of a single frequency in the audio input and compare it to a detection threshold. This can be done by computing the Fourier transform at a single frequency value, the one of the CTCSS subtone. The Goertzel algorithm provides an elegant solution to this problem. By sampling the audio input x at a sampling rate of a multiple p of the tone frequency, and over a buffer length of N period (thus sampling N.p points), the Goertzel algorithm computes a sequence s such as:
We can then calculate the power term as:
The tricky thing to do on a 8-bit micro-controller with no floating-point arithmetic (and no machine instruction for division for that matter) is the multiplication by the constant cos(2π/p). Fixed point arithmetic is out of question because for p much larger than one – which is required to avoid potential aliasing caused by higher frequency tones, cos(2π/p) is fairly closed to 1 and the error would accumulate. The trick to speed up the calculation is to find a couple of integers p and Ω such as:
Values of p=201 and Ω=11 are a surprisingly good approximation (the correct value of p is 201.054). This allows the computation to be done solely with integer addition, subtraction and bit shifting:
#define COEFF_MULT(x) (((x) << 1) - ((x) >> (OMEGA_FACTOR - 1)))
volatile int32_t sprev, sprev2;
volatile uint16_t sample_no = 0;
ISR(ADC_vect) {
int32_t s = (int32_t)ADC + COEFF_MULT(sprev) - sprev2;
sprev2 = sprev;
sprev = s;
sample_no++;
if (sample_no >= NUMBER_OF_PERIODS * P_FACTOR) {
// Power term calculation...
sprev = sprev2 = 0;
sample_no = 0;
}
}Note that’s also the reason why the encoder output frequency is 201 times the CTCSS tone: both encoding and decoding use the same timer in the same configuration. The decoding is performed over 32 tone periods (478ms at the lowest tone and 126ms at the highest one), as a compromise between tone separation, signal/noise separation and detection speed.
End result
Here is the little board:

I first check the quality of the generated tone, to check that the generated frequency was correct and the waveform had a good sine shape. The result was quite satisfying, with no measurable harmonics.
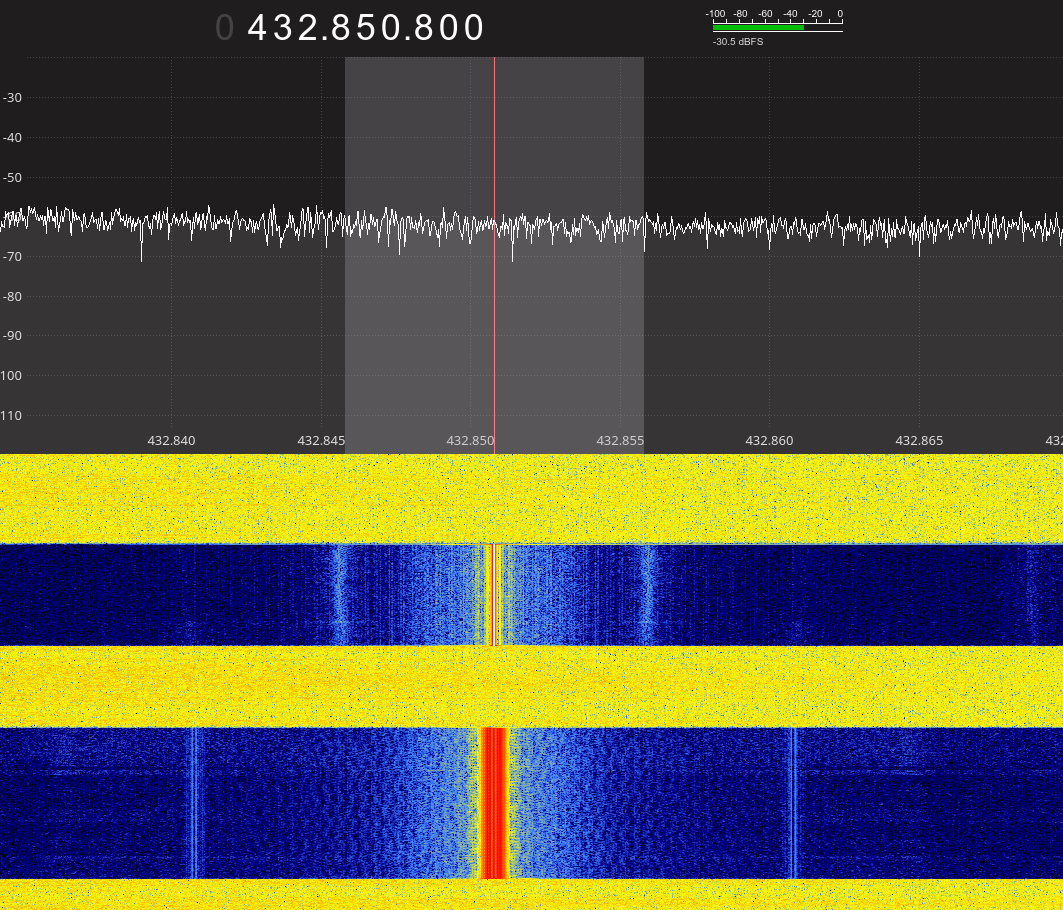
Once properly installed on my Yaesu FT-736M, I checked the proper deviation of the encoder by checking the emission of the transmitter using a RTL-SDR dongle and Gqrx software. The following screenshot show the transmitter output with CTCSS encoding enabled (bottom waterfall) and without (top). The deviation is about 15-20% of the signal range, which is what is expected for a CTCSS tone.
I checked the tone squelch feature of two ways communications by using an handheld transceiver and checking that both and trigger the CTCSS tone detection of the other.
The code is uploaded on my Github page and is licensed under the GPL v3 license (opensource).
I had to build 5 of those (which was the minimum order quantity), so I have 4 of those for sale on eBay for anyone interested.
EDIT: I ordered some more since it appears that those board were of interest to several OM. They are for sales on eBay.
EDIT2: New eBay link : https://www.ebay.fr/itm/186906777747
References
- CTCSS wikipedia page: https://en.wikipedia.org/wiki/Continuous_Tone-Coded_Squelch_System
- A homemade replacement for the FTS-8 subtone encoder by homo ludens: https://ludens.cl/Electron/fts8/fts8.html
- ZL2PD Multi-Map CTCSS Encoder – Emulating CML or MX-Com or Panasonic or Seiko CTCSS Encoders by ZL2PD: https://www.zl2pd.com/CML_PW_50tone_CTCSS_Encoder.html
- Developing a Flexible CTCSS Decoder by ZL2PD : https://www.zl2pd.com/CTCSS_Decoder.html
F4VQG
Developing a replacement for the FTS-8 CTCSS sub-tone encoder/decoder
Do you have 1 pcs of this for me?
Best regards
Hi Walter. Yes, I put some on sales on eBay: https://www.ebay.fr/itm/326246363054
Cheers